

The domain and range of such a function will come out to be:Īs the function is linear, the graph would come out to be a line. Domain of a quadratic functionįurther, upon observation, there are not any x-values that will make the function not exist or invalid since no denominator or square root exists.
The equation given is clearly a purely linear equation which implies the coefficient of the square power is 0.

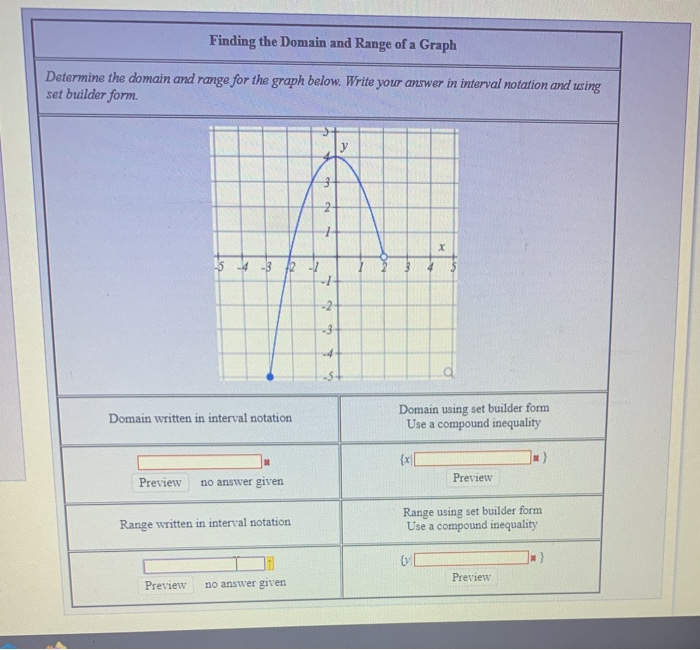
Example 1įind the domain and range of the linear function Here are some examples on domain and range of a parabola.
#DOMAIN AND RANGE CALCULATOR HOW TO#
Let us have a step by step guidance on how to find the domain and range of a quadratic function. How to find the domain and range of a quadratic function? So it is important for us to see the domain and range of a quadratic function to really understand the domain and range of a parabola. Upon rearranging the terms, it comes out to be a quadratic function. Let us verify whether the relation between height and time is quadratic by looking at the vertical equation for projectile motion that deals with position and time:ĭoes it look familiar? Let's try rearranging the equation a bit: We can see our graph creates an upside-down parabola, which is the sort of thing you might expect from a quadratic relation. Over time the ball goes up to a maximum height, and then back down to the starting height again when you catch it. Let's try visualizing this with a height vs. Think that you're tossing a baseball straight up in the air. In many places, you'll encounter a quadratic relation in physics with projectile motion. And one of its important characteristics is how to find the domain and range of a quadratic function or domain and range of a parabola in other words. In the amazing world of algebra, there is a fascinating topic called Quadratic functions.įun explodes with the solving of equations, making graphs along with understanding the real-life and practical use of this function. Here, we'll go over both quadratic relationships, and a couple of examples of finding domain and range of a quadratic function. There are four different common relationships between variables you're sure to run into: they're linear, direct, quadratic, and inverse relationships.


 0 kommentar(er)
0 kommentar(er)
